Rotating Magnetic Field: Derivation, conditions, and definition

Add a comment

The rotating magnetic field can be defined as the field or flux having constant amplitude but whose axis is continuously rotating in a plane with a certain speed. So if the arrangement is made to rotate a permanent magnet, then the resulting field is a rotating magnetic field.

In three phase induction motors such a rotating magnetic field is produced by supplying currents to a set of stationary windings, with the help of three phase a.c. supply.

The current carrying windings produce the magnetic field or flux. And due to interaction of three fluxes produced due to three phase supply, resultant flux has a constant magnitude and its axis rotating in space without physically rotating the windings. This type of field is nothing but rotating magnetic field.

Production of Rotating Magnetic Field (RMF)

There are two conditions exist for the production of a Rotating Magnetic field:

  1.  A three phase induction motor consists of three phase winding as its stationary part called Stator. The three phase stator winding is connected in star or delta. The three phase windings are displaced from each other by 120^{\circ}
  2. The windings are supplied by a balanced 3 phase a.c. supply (Means electrically 120^{\circ} apart from each other).

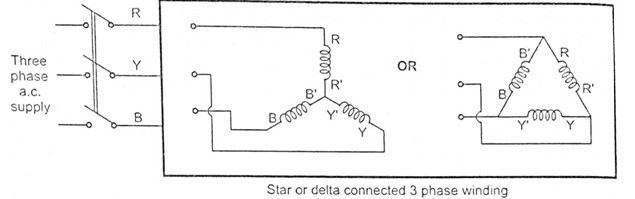
induction1

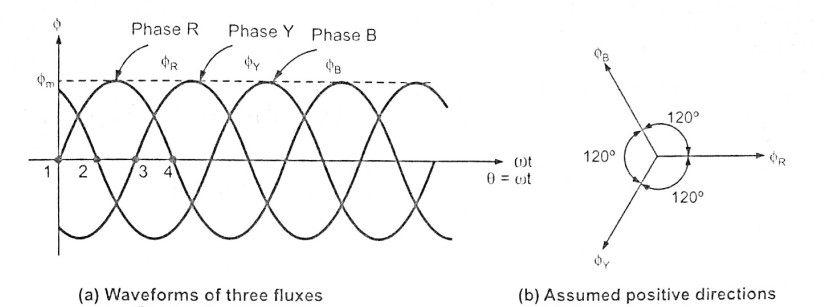
The three phase currents flow simultaneously through the windings and are displaced from each other by 120^{\circ} electrical. Each alternating phase current produces its own flux which is sinusoidal. So all three fluxes are sinusoidal and are separated from each other by 120^{\circ} degree. If the phase sequence of the windings is R-Y-B , then mathematical equations for the instantaneous values of the three fluxes \phi_{R}, \; \phi_{B}, \; \phi_{Y} can be written as, (The flux \phi_{R} is taken as the reference phasor):

\phi_{R} = \phi_{m} \; \sin (\omega t) = \phi_{m} \; \sin {(\theta)}

\phi_{Y} = \phi_{m} \; \sin (\omega t - 120^{\circ}) = \phi_{m} \; \sin {(\theta - 120^{\circ})}

\phi_{B} = \phi_{m} \; \sin (\omega t - 240^{\circ}) = \phi_{m} \; \sin {(\theta - 240^{\circ})}

As windings are identical and supply is balanced, the amplitude of each flux is \phi_{m} . Due to phase sequence R-Y-B , flux \phi_{Y} lags behind \phi_{R} by 120^{\circ} and \phi_{B}   lags \phi_{Y}  by 120^{\circ} . So \phi_{B} ultimately lags \phi_{R} by 240^{\circ} .

induction2

Let \phi_{R}, \; \phi_{B}, \; \phi_{Y} \; be the instantaneous values of these three fluxes. The resultant flux is the phasor addition of \phi_{R}, \; \phi_{B}, \; \phi_{Y} .

\boxed {\phi_{T} = \phi_{R} + \phi_{B} + \phi_{Y}}

Case (1): When (\theta = 0^{\circ})

\phi_{R} = \phi_{m} \; \sin {0^{\circ}} = 0

\phi_{Y} = \phi_{m} \; \sin {(-120^{\circ})} = - \; 0.866 \; \phi_{m}

\phi_{B} = \phi_{m} \; \sin {(-240^{\circ})} = + \; 0.866 \; \phi_{m}

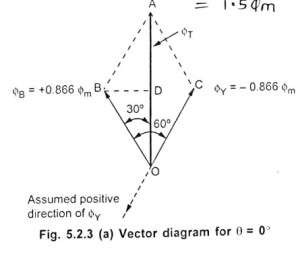
induction3

The phasor addition is shown in the figure. \text {BD} is drawn perpendicular from \text {B} on \phi_{T} . It bisects \phi_{T} .

\text {OD} = \text {DA} = \left( \dfrac {\phi_{T}}{2} \right)

In triangle \text {OBD} , angle \; \text {BOD} = 30^{\circ}

\cos {30^{\circ}} = \dfrac {\text {OD}}{\text {OB}} = \dfrac {\left( \dfrac {\phi_{T}}{2} \right)}{0.866 \; \phi_{m}}

\Longrightarrow \boxed {\phi_{T} = 2 \times 0.866 \; \phi_{m} \times \cos {30^{\circ}} = 1.5 \; \phi_{m}}

So magnitude of \phi_{T} is 1.5 \; \phi_{m} and its position is vertically upwards at \theta = 0^{\circ} .

Case (2): When 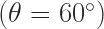(\theta = 60^{\circ})

\phi_{R} = \phi_{m} \; \sin {60^{\circ}} = + \; 0.866 \; \phi_{m}

\phi_{Y} = \phi_{m} \; \sin {(-60^{\circ})} = - \; 0.866 \; \phi_{m}

\phi_{B} = \phi_{m} \; \sin {(-180^{\circ})} = 0

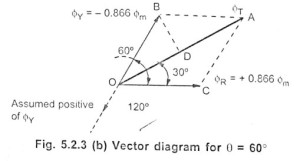
induction4

So \phi_{R} is positive and \phi_{Y}   is negative and hence drawing in appropriate directions we phasor diagram as shown in figure.

Doing the same construction, drawing perpendicular from B on \phi_{T} at D we get the same results.

\boxed {\phi_{T} = 1.5 \; \phi_{m}}

But it can be seen that though its magnitude is 1.5 \; \phi_{m} it has rotated through 60^{\circ} in space, in clockwise direction, from its previous position. 

Case (3): When 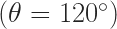(\theta = 120^{\circ})

\phi_{R} = \phi_{m} \; \sin {120^{\circ}} = + \; 0.866 \; \phi_{m}

\phi_{Y} = \phi_{m} \; \sin {(0^{\circ})} = 0

\phi_{B} = \phi_{m} \; \sin {(-60^{\circ})} = - \; 0.866 \; \phi_{m}

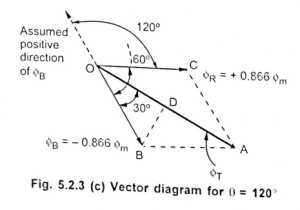
induction5

After doing the same construction as before it can be proved again that,

\boxed {\phi_{T} = 1.5 \; \phi_{m}}

But it can be seen that though its magnitude is 1.5 \; \phi_{m} it has rotated through 120^{\circ} in space, in clockwise direction, from its 1st position \theta = 0^{\circ} . 

Magnitude of the net flux remains same, but it can be seen that it has further rotated through 60∘ from its previous position in clockwise direction.

Leave a comment